[R][python] bootstrap, 신뢰 구간(CI, confidence interval)

fig 1. title

bootstrap을 이용해서 신뢰 구간(CI, confidence interval) 구하기

 

0. background

1. bootstrap

2. R에서 bootstrap을 이용해서 신뢰구간 구하기

3. python에서 bootstrap을 이용해서 신뢰구간 구하기

---

0. background

 

- machine learning 모델들의 성능비교에 신뢰 구간은 필수적.

- 흔히 AUROC나 sensitivity, specificity 같은 지표들이 성능 평가에 사용됨.

- 성능 지표들에 따라 여러 통계기법들이 사용되고 있음.

- data science는 많은 샘플링이 가능하기 때문에 bootstrap 방법으로 여러 샘플링을 할 수 있음.

- bootstrap 방법으로 신뢰 구간을 구해 볼거임.

- R에서는 "pROC" 패키지를 통해 간단하게 계산 할 수 있음.

  -> 하지만 sample_weight가 적용된 모델에 대한 신뢰 구간을 구하는데는 한계가 있음.

- python에서는 scikit-learn의 유틸 조합으로 sample_weight가 적용된 모델의 신뢰 구간 계산이 가능함.

---

1. bootstrap

 

fig 2. bootstrap. 출처 : https://arifromadhan19.medium.com/resampling-methods-a-simple-introduction-to-the-bootstrap-method-3a36d076852f

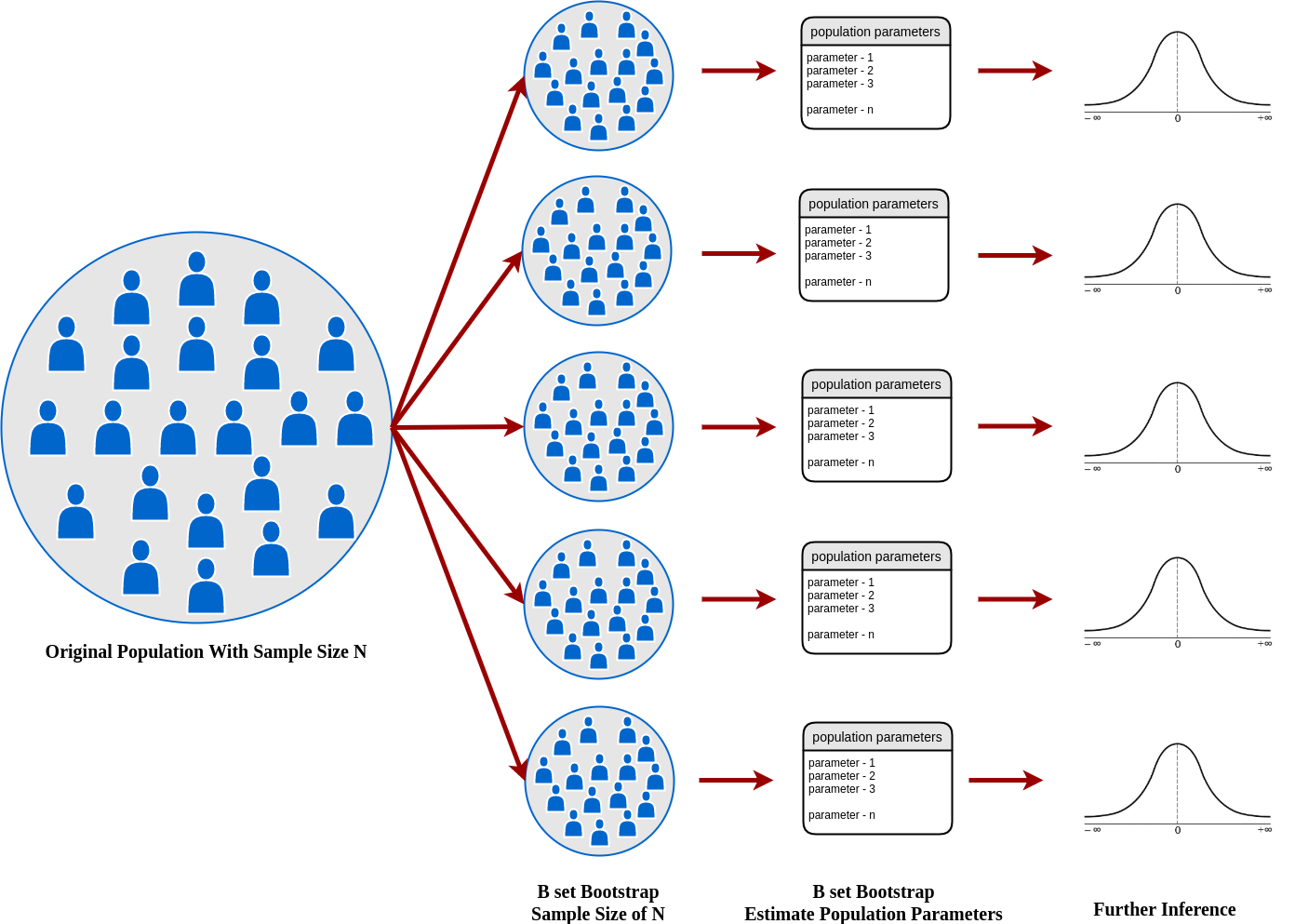
- 간단히 요약해서 전체데이터에서 중복을 허용하여 모집단과 같은 size로 원하는 수 만큼 샘플링을 하는것.

- 원하는 수 만큼 샘플링한 모든 데이터의 수치에서 2.5%, 50%, 97.5%를 취함(95% Confidence Interval).

- 보통 2000번정도 하는 것을 권장하지만 10000번 정도 이상하면 좋음.

- clinical 에서 신뢰 구간을 구하는 데 굉장히 powerful한 방법으로 통함.

 

참고 : https://arifromadhan19.medium.com/resampling-methods-a-simple-introduction-to-the-bootstrap-method-3a36d076852f

Resampling Methods — A Simple Introduction to The Bootstrap Method

참고 : https://projecteuclid.org/journals/statistical-science/volume-11/issue-3/Bootstrap-confidence-intervals/10.1214/ss/1032280214.full

Bootstrap confidence intervals

---

2. R에서 bootstrap을 이용해서 신뢰구간 구하기

 

- R에서는 "pROC"를 이용해서 여러 기법들을 이용해서 쉽게 신뢰 구간을 계산할 수 있음.

- method를 bootstrap으로 변경해주면 됨.

##auc delong
print("delong auc"); ci.auc(df$label, df$probability)

##auc bootstrap
print("bootstrap auc"); ci.auc(df$label, df$probability, method="bootstrap", boot.n=2000)

##fixed threshold se, sp
print("se, sp in fixed best threshold"); ci.thresholds(roc(dfp$label, df$probability), thresholds = 0.5, conf.level = 0.95, boot.n=2000)

##th, se, sp bootstrap
ci.coords(roc(df$label, df$probability), x="best", ret=c("threshold", "sensitivity", "specificity"), boot.n = 2000)

참고 : https://www.rdocumentation.org/packages/pROC/versions/1.17.0.1

pROC package - RDocumentation

---

3. python에서 bootstrap을 이용해서 신뢰구간 구하기

 

- python에서는 scikit-learn의 툴을 조합해서 사용할 수 있음.

- "resample"을 중복을 허용하게(replace=TRUE) 원하는 샘플 수 만큼 시행.

- 샘플마다 모든 지표들을 구하고 해당 지표의 2.5%, 50%, 97.5%의 값을 가져옴.

- 무엇보다 "sample_weight" 옵션을 사용할 수 있는 것이 강점.

  -> weighted AUROC나 weighted sensitivity, weighted specificity를 구할 수 있음.

# weighted CI

# load dataset
data = df

# configure bootstrap
n_iterations = 2000
n_size = len(data)

# run bootstrap
auc_box = []
th_box = []
se_box = []
sp_box = []

for i in range(n_iterations):
    boot = resample(data, n_samples=n_size, replace=True, stratify=data['label'])
    auc = roc_auc_score(boot['label'], boot['prob'], sample_weight=boot['wt'])
    
    auc_box.append(auc)
    
    # calculate roc curves
    fpr, tpr, thresholds = roc_curve(boot['label'], boot['prob'], sample_weight=boot['wt'])
    J = tpr - fpr
    ix = argmax(J)
    best_thresh, se, sp = thresholds[ix], tpr[ix], 1-fpr[ix]
    
    th_box.append(best_thresh)
    se_box.append(se)
    sp_box.append(sp)
    
# plot scores
plt.hist(auc_box)
plt.hist(th_box)
plt.hist(se_box)
plt.hist(sp_box)
plt.show()

# confidence intervals
alpha = 0.95
p = ((1.0-alpha)/2.0) * 100
lower_auc = max(0.0, np.percentile(auc_box, p))
p = (alpha+((1.0-alpha)/2.0)) *100
upper_auc = min(1.0, np.percentile(auc_box, p))
print('auc mean:%.3f, median:%.3f, CI %.3f - %.3f' % (mean(auc_box), np.median(auc_box), lower_auc, upper_auc))

p = ((1.0-alpha)/2.0) * 100
lower_th = max(0.0, np.percentile(th_box, p))
p = (alpha+((1.0-alpha)/2.0)) *100
upper_th = min(1.0, np.percentile(th_box, p))
print('th mean:%.3f, median:%.3f, CI %.3f - %.3f' % (mean(th_box), np.median(th_box), lower_th, upper_th))

p = ((1.0-alpha)/2.0) * 100
lower_se = max(0.0, np.percentile(se_box, p))
p = (alpha+((1.0-alpha)/2.0)) *100
upper_se = min(1.0, np.percentile(se_box, p))
print('se mean:%.3f, median:%.3f, CI %.3f - %.3f' % (mean(se_box), np.median(se_box), lower_se, upper_se))

p = ((1.0-alpha)/2.0) * 100
lower_sp = max(0.0, np.percentile(sp_box, p))
p = (alpha+((1.0-alpha)/2.0)) *100
upper_sp = min(1.0, np.percentile(sp_box, p))
print('sp mean:%.3f, median:%.3f, CI %.3f - %.3f' % (mean(sp_box), np.median(sp_box), lower_sp, upper_sp))

참고 : https://machinelearningmastery.com/calculate-bootstrap-confidence-intervals-machine-learning-results-python/

How to Calculate Bootstrap Confidence Intervals For Machine Learning Results in Python